Fun with vectors in the Raspberry Pi 1 - Part 1
Long ago, we saw that the Raspberry Pi 1 has vector computation capabilities. However to the best of my knowledge no compiler attempted to exploit the vector capability in general.
I think we are going to have some fun in trying to fix this.
A bit of a reminder
The Raspberry Pi 1 comes with a BCM2835 SoC that includes a ARM1176JZF-S core. This core implements the ARMv6 architecture and includes support for floating point operations via an extension of ARMv6 that was commercially called VFP. VFP had several versions but the one included in the ARM1176JZF-S core is VFPv2.
VFP provides 32 registers of single precison which can be grouped in pairs to provide 16 registers of double precision.
However the registers are grouped in banks, a first scalar bank and three vector banks.
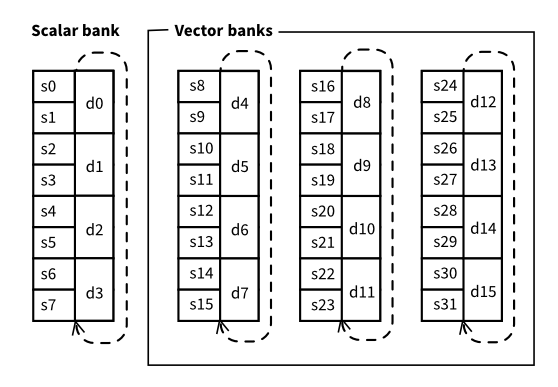
The fpscr register has a field called len that encodes the vector length.
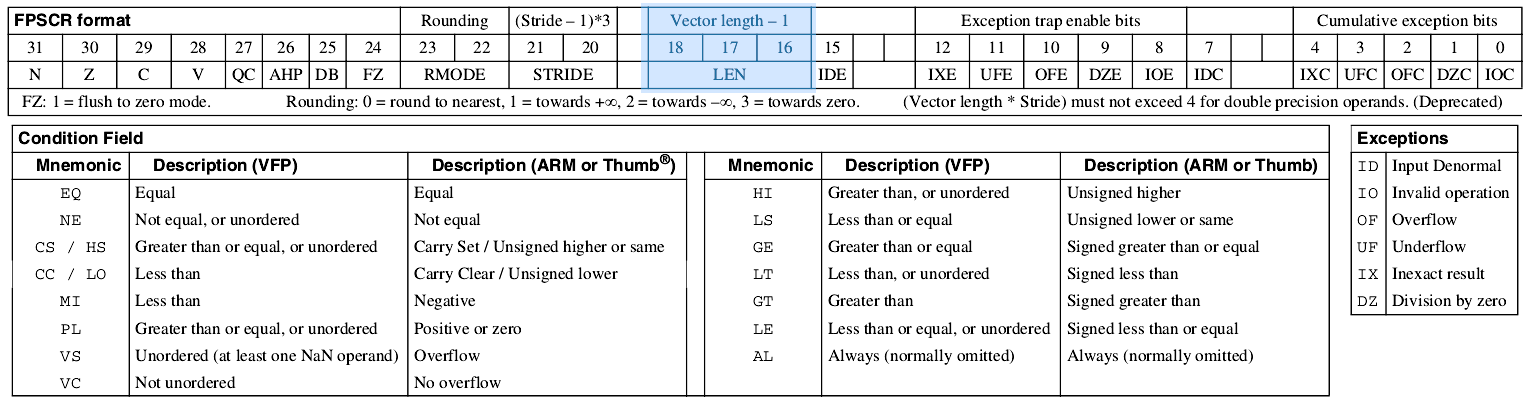
fpscr register.
Image from Vector Floating Point Instruction Set Quick Reference Card.By default the vector length is set to 1 (encoded as 0b000 in the len field
of fpscr) and so all the operations with all the registers are regular scalar
floating point operations, regardless of the bank they are found in.
However if we set len to a value larger than 1, typically 2 or 4 but it is
possible to use any value from 2 to 8, the behaviour changes for a few
instructions. If the operands only involve registers in the scalar bank,
then they will continue computing scalar values.
# vector length is 3
vfadd.f32 s2, s4, s5
# s2 ← s4 + s5If the operands involve registers in the vector banks, the computation will be
extended to the next len registers, wrapping around inside the bank if
needed.
# vector length is 3
vfadd.f32 s9, s17 s30
# s9 ← s17 + s30
# s10 ← s18 + s31
# s11 ← s19 + s24Finally there is a mixed mode where one source register is in the scalar bank
and the other one in a vector bank, the value of the scalar bank will be reused
len times as operand of each vec
# vector length is 3
vfadd.f32 s9, s4 s30
# s9 ← s4 + s30
# s10 ← s4 + s31
# s11 ← s4 + s24Finally note that not all the instructions honour len. Only the following
instructions do:
| Instruction | Meaning | Notes |
|---|---|---|
vadd.<ty> a, b, c |
a ← b + c |
|
vsub.<ty> a, b, c |
a ← b - c |
|
vmul.<ty> a, b, c |
a ← b * c |
|
vnmul.<ty> a, b, c |
a ← -(b * c) |
|
vdiv.<ty> a, b, c |
a ← b / c |
|
vmla.<ty> a, b, c |
a ← a + (b * c) |
Different rounding to vmul followed by vadd |
vmls.<ty> a, b, c |
a ← a - (b * c) |
Ditto. |
vnmla.<ty> a, b, c |
a ← -a - (b * c) |
Ditto. |
vnmls.<ty> a, b, c |
a ← -a + (b * c) |
Ditto. |
vneg.<ty> a, b |
a ← -b |
|
vabs.<ty> a, b |
a ← |b| |
|
vsqrt.<ty> a, b |
a ← √b |
Modelling in LLVM
Before we can even try to generate code, we need to think a bit how to model the vector computation in the LLVM infrastructure.
Types
LLVM IR supports vector types of the form <k x ty> where k is a constant
and ty is the base type of the vector. In our case ty is either going to be
double (called f64 in the code generator of LLVM) and float (called f32
in the code generator).
Technically speaking we could support a range of vector types, specially
for float from 2 to 8, as in <2 x float>, <3 x float>, etc. However
non-power of 2 vector lengths are a bit unusual. In fact the vectorizer of
LLVM currently only considers powers of two. To avoid complicating ourselves
a lot, we will consider only <2 x double> and <4 x float>.
Technically speaking, <4 x double> is something we could consider too.
However if you look at the register banks above you will see that in practice
we can only represent 3 of those vectors at a time. A few algorithms can live
with this but it will be often too limiting.
Registers
Now the next step is thinking what storage we are going to use to represent those vectors.
If you look closely at the table above and given the behaviour of VFP, any
consecutive pair of d<n> registers within the same bank can be used for <2 x
double>. This means that (d4, d5), (d5, d6), (d6, d7) and (d7,d4) are
four options available in the first bank. Note that the pair (d5, d6) may
feel a bit suboptimal but we still can use (d7, d4) if needed. LLVM knows when
two groups of registers overlap, so in principle we can give all the options
and let LLVM generate correct code.
We will see later than some other parts of VFP will lead us to prefer pairs
whose first component is an even numbered d<n> register. It is also possible
to suggest LLVM to prefer some specific order for registers.
A similar rationale applies for <4 x float> but this time it will be groups
of 4 consecutive (including the wrap-around within the bank) s<n> registers.
So for instance (s8, s9, s10, 11) but also (s14, s15, s8, s9). Similarly
groups whose first s<n> register is a multiple of four will be preferable.
Effectively, not counting overlaps, VFPv2 provides us with the following resources:
| Type | Number of registers |
|---|---|
<2 x double> |
6 |
<4 x float> |
12 |
Operations
LLVM IR does not have explicit operations for all the instructions above but it
will be relatively easy to pattern match them when possible. For instance if we
are happy with floating-point contraction (i.e. we don’t care about all the
roundings that IEEE 754 might require) a vmla.<ty> instruction can be used
when the program wants to compute a + (b * c)
The contentious part, however, is that we need to make sure the field len of
the fpscr register is correctly set.
The following LLVM IR means add two vectors of type <2 x double>. The
operands of this operation are represented by values %va and %vb. The
result of the operation is represented by %vc.
%vc = fadd <2 x double> %va, %vbNote however that VFP also supports scalar operations and LLVM lowers them to those instructions. So a piece of IR like the following one
%c = fadd double %a, %bmay be lowered into the following instruction
vadd.f64 d2, d3, d8This is correct because the state of the program is assumed to be such that
the len field is always 0.
However, because we want to use vectors, we are about to break this assumption.
This means that our program will need to ensure that the len field has the
right value before executing the corresponding instruction: scalar or vector.
We will see that maintaining this invariant when generating code is going to
give us some headaches. These sort of designs actually complicate compilers.
Now a compiler needs to introduce computation that sets
the CPU state (in our case the len field) as needed but at the same time
we want it to do it in the most efficient way possible (i.e. avoiding resetting
the CPU state more than it is needed).
VFP will help us a bit because not all the operations will care about the
len field so we will have a bit of leeway here.
Goal
Our first goal is to add enough functionality to LLVM so the following hello world of vectorization:
void vadd_f32(float *restrict c, float *restrict a, float *restrict b, int n) {
for (int i = 0; i < n; i++) {
c[i] = a[i] + b[i];
}
}is emitted like this:
⋮
@ %bb.2: @ %vector.ph
vmrs r4, fpscr @ \
mvn r7, #458752 @ |
and r4, r4, r7 @ |
mov r7, #196608 @ | Sets the vector length to 4
orr r4, r4, r7 @ |
vmsr fpscr, r4 @ /
.LBB0_3: @ %vector.body
@ =>This Inner Loop Header: Depth=1
vldmia r6, {s8, s9, s10, s11} @ Loads b[i : i + 3]
vldmia r5, {s12, s13, s14, s15} @ Loads a[i : i + 3]
vadd.f32 s8, s12, s8 @ Computes a[i : i + 3] + b[i : i + 3]
subs lr, lr, #4
add r5, r5, #16
add r6, r6, #16
vstmia r8!, {s8, s9, s10, s11} @ Stores into c[i : i + 3]
bne .LBB0_3
⋮Is any of this useful?
The VFP architecture was intended to support execution of short “vector mode” instructions but these operated on each vector element sequentially and thus did not offer the performance of true single instruction, multiple data (SIMD) vector parallelism. This vector mode was therefore removed shortly after its introduction, to be replaced with the much more powerful Advanced SIMD, also known as Neon.
I don’t expect any performance improvement when using vector operations in the Raspberry Pi 1. In fact the only metric we may possibly improve is code size. It is going to be fun anyways.
And that should be it for today. The rest of the chapters will be more deep down how we can hammer LLVM so it emits vector code for the Raspberry Pi 1.