ARM assembler in Raspberry Pi – Chapter 13
So far, all examples have dealt with integer values. But processors would be rather limited if they were only able to work with integer values. Fortunately they can work with floating point numbers. In this chapter we will see how we can use the floating point facilities of our Raspberry Pi.
Floating point numbers
Following is a quick recap of what is a floating point number.
A binary floating point number is an approximate representation of a real number with three parts: sign, mantissa and exponent. The sign may be just 0 or 1, meaning 1 a negative number, positive otherwise. The mantissa represents a fractional magnitude. Similarly to 1.2345 we can have a binary 1.01110 where every digit is just a bit. The dot means where the integer part ends and the fractional part starts. Note that there is nothing special in binary fractional numbers: 1.01110 is just 20 + 2-2 + 2-3 + 2-4 = 1.43750(10. Usually numbers are normalized, this means that the mantissa is adjusted so the integer part is always 1, so instead of 0.00110101 we would represent 1.101101 (in fact a floating point may be a denormal if this property does not hold, but such numbers lie in a very specific range so we can ignore them here). If the mantissa is adjusted so it always has a single 1 as the integer part two things happen. First, we do not represent the integer part (as it is always 1 in normalized numbers). Second, to make things sound we need an exponent which compensates the mantissa being normalized. This means that the number -101.110111 (remember that it is a binary real number) will be represented by a sign = 1, mantissa = 1.01110111 and exponent = 2 (because we moved the dot 2 digits to the left). Similarly, number 0.0010110111 is represented with a sign = 0, mantissa = 1.0110111 and exponent = -3 (we moved the dot 3 digits to the right).
In order for different computers to be able to share floating point numbers, IEEE 754 standardizes the format of a floating point number. VFPv2 supports two of the IEEE 754 numbers: Binary32 and Binary64, usually known by their C types, float and double, or by single- and double-precision, respectively. In a single-precision floating point the mantissa is 23 bits (+1 of the integer one for normalized numbers) and the exponent is 8 bits (so the exponent ranges from -126 to 127). In a double-precision floating point the mantissa is 52 bits (+1) and the exponent is 11 bits (so the exponent ranges from -1022 to 1023). A single-precision floating point number occupies 32 bit and a double-precision floating point number occupies 64 bits. Operating double-precision numbers is in average one and a half to twice slower than single-precision.
Goldberg's famous paper is a classical reference that should be read by anyone serious when using floating point numbers.
Coprocessors
As I stated several times in earlier chapters, ARM was designed to be very flexible. We can see this in the fact that ARM architecture provides a generic coprocessor interface. Manufacturers of system-on-chips may bundle additional coprocessors. Each coprocessor is identified by a number and provides specific instructions. For instance the Raspberry Pi SoC is a BCM2835 which provides a multimedia coprocessor (which we will not discuss here).
That said, there are two standard coprocessors in the ARMv6 architecture: 10 and 11. These two coprocessors provide floating point support for single and double precision, respectively. Although the floating point instructions have their own specific names, they are actually mapped to generic coprocessor instructions targeting coprocessor 10 and 11.
Vector Floating-point v2
ARMv6 defines a floating point subarchitecture called the Vector Floating-point v2 (VFPv2). Version 2 because earlier ARM architectures supported a simpler form called now v1. As stated above, the VFP is implemented on top of two standarized coprocessors 10 and 11. ARMv6 does not require VFPv2 be implemented in hardware (one can always resort to a slower software implementation). Fortunately, the Raspberry Pi does provide a hardware implementation of VFPv2.
VFPv2 Registers
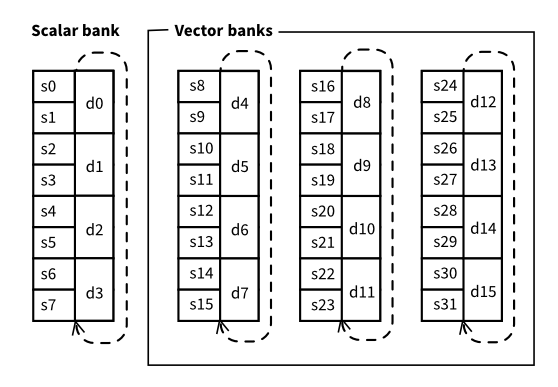
We already know that the ARM architecture provides 16 general purpose registers r0 to r15, where some of them play special roles: r13, r14 and r15. Despite their name, these general purpose registers do not allow operating floating point numbers in them, so VFPv2 provides us with some specific registers. These registers are named s0 to s31, for single-precision, and d0 to d15 for double precision. These are not 48 different registers. Instead every dn is mapped to two (consecutive) registers s2n and s2n+1, where 0 ≤ n ≤ 15.
These registers are structured in 4 banks: s0-s7 (d0-d3), s8-s15 (d4-d7), s16-s23 (d8-d11) and s24-s31 (d12-d15). We will call the first bank (bank 0, s0-s7, d0-d3) the scalar bank, while the remaining three are vectorial banks (below we will see why).
VFPv2 provides three control registers but we will only be interested in one called fpscr. This register is similar to the cpsr as it keeps the usual comparison flags N, Z, C and V. It also stores two fields that are very useful, len and stride. These two fields control how floating point instructions behave. We will not care very much of the remaining information in this register: status information of the floating point exceptions, the current rounding mode and whether denormal numbers are flushed to zero.
Arithmetic operations
Most VFPv2 instructions are of the form vname Rdest, Rsource1, Rsource2 or fname Rdest, Rsource1. They have three modes of operation.
- Scalar. This mode is used when the destination register is in bank 0 (
s0-s7ord0-d3). In this case, the instruction operates only withRsource1andRsource2. No other registers are involved. - Vectorial. This mode is used when the destination register and Rsource2 (or Rsource1 for instructions with only one source register) are not in the bank 0. In this case the instruction will operate as many registers (starting from the given register in the instruction and wrapping around the bank of the register) as defined in field
lenof thefpscr(at least 1). The next register operated is defined by thestridefield of thefpscr(at least 1). If wrap-around happens, no register can be operated twice. - Scalar expanded (also called mixed vector/scalar). This mode is used if Rsource2 (or Rsource1 if the instruction only has one source register) is in the bank0, but the destination is not. In this case Rsource2 (or Rsource1 for instructions with only one source) is left fixed as the source. The remaining registers are operated as in the vectorial case (this is, using
lenandstridefrom thefpscr).
Ok, this looks pretty complicated, so let's see some examples. Most instructions end in .f32 if they operate on single-precision and in .f64 if they operate in double-precision. We can add two single-precision numbers using vadd.f32 Rdest, Rsource1, Rsource2 and double-precision using vadd.f64 Rdest, Rsource1, Rsource2. Note also that we can use predication in these instructions (but be aware that, as usual, predication uses the flags in cpsr not in fpscr). Predication would be specified before the suffix like in vaddne.f32.
// For this example assume that len = 4, stride = 2
vadd.f32 s1, s2, s3 /* s1 ← s2 + s3. Scalar operation because Rdest = s1 in the bank 0 */
vadd.f32 s1, s8, s15 /* s1 ← s8 + s15. ditto */
vadd.f32 s8, s16, s24 /* s8 ← s16 + s24
s10 ← s18 + s26
s12 ← s20 + s28
s14 ← s22 + s30
or more compactly {s8,s10,s12,s14} ← {s16,s18,s20,s22} + {s24,s26,s28,s30}
Vectorial, since Rdest and Rsource2 are not in bank 0
*/
vadd.f32 s10, s16, s24 /* {s10,s12,s14,s8} ← {s16,s18,s20,s22} + {s24,s26,s28,s30}.
Vectorial, but note the wraparound inside the bank after s14.
*/
vadd.f32 s8, s16, s3 /* {s8,s10,s12,s14} ← {s16,s18,s20,s22} + {s3,s3,s3,s3}
Scalar expanded since Rsource2 is in the bank 0
*/Load and store
Once we have a rough idea of how we can operate floating points in VFPv2, a question remains: how do we load/store floating point values from/to memory? VFPv2 provides several specific load/store instructions.
We load/store one single-precision floating point using vldr/vstr. The address of the load/store must be already in a general purpose register, although we can apply an offset in bytes which must be a multiple of 4 (this applies to double-precision as well).
vldr s1, [r3] /* s1 ← *r3 */
vldr s2, [r3, #4] /* s2 ← *(r3 + 4) */
vldr s3, [r3, #8] /* s3 ← *(r3 + 8) */
vldr s4, [r3, #12] /* s4 ← *(r3 + 12) */
vstr s10, [r4] /* *r4 ← s10 */
vstr s11, [r4, #4] /* *(r4 + 4) ← s11 */
vstr s12, [r4, #8] /* *(r4 + 8) ← s12 */
vstr s13, [r4, #12] /* *(r4 + 12) ← s13 */We can load/store several registers with a single instruction. In contrast to general load/store, we cannot load an arbitrary set of registers but instead they must be a sequential set of registers.
// Here precision can be s or d for single-precision and double-precision
// floating-point-register-set is {sFirst-sLast} for single-precision
// and {dFirst-dLast} for double-precision
vldm indexing-mode precision Rbase{!}, floating-point-register-set
vstm indexing-mode precision Rbase{!}, floating-point-register-setThe behaviour is similar to the indexing modes we saw in chapter 10. There is a Rbase register used as the base address of several load/store to/from floating point registers. There are only two indexing modes: increment after and decrement before. When using increment after, the address used to load/store the floating point value register is increased by 4 after the load/store has happened. When using decrement before, the base address is first subtracted as many bytes as foating point values are going to be loaded/stored. Rbase is always updated in decrement before but it is optional to update it in increment after.
vldmias r4, {s3-s8} /* s3 ← *r4
s4 ← *(r4 + 4)
s5 ← *(r4 + 8)
s6 ← *(r4 + 12)
s7 ← *(r4 + 16)
s8 ← *(r4 + 20)
*/
vldmias r4!, {s3-s8} /* Like the previous instruction
but at the end r4 ← r4 + 24
*/
vstmdbs r5!, {s12-s13} /* *(r5 - 4 * 2) ← s12
*(r5 - 4 * 1) ← s13
r5 ← r5 - 4*2
*/
For the usual stack operations when we push onto the stack several floating point registers we will use vstmdb with sp! as the base register. To pop from the stack we will use vldmia again with sp! as the base register. Given that these instructions names are very hard to remember we can use the mnemonics vpush and vpop, respectively.
vpush {s0-s5} /* Equivalent to vstmdb sp!, {s0-s5} */
vpop {s0-s5} /* Equivalent to vldmia sp!, {s0-s5} */Movements between registers
Another operation that may be required sometimes is moving among registers. Similar to the mov instruction for general purpose registers there is the vmov instruction. Several movements are possible.
We can move floating point values between two floating point registers of the same precision
vmov s2, s3 /* s2 ← s3 */Between one general purpose register and one single-precision register. But note that data is not converted. Only bits are copied around, so be aware of not mixing floating point values with integer instructions or the other way round.
vmov s2, r3 /* s2 ← r3 */
vmov r4, s5 /* r4 ← s5 */Like the previous case but between two general purpose registers and two consecutive single-precision registers.
vmov s2, s3, r4, r10 /* s2 ← r4
s3 ← r10 */Between two general purpose registers and one double-precision register. Again, note that data is not converted.
vmov d3, r4, r6 /* Lower32BitsOf(d3) ← r4
Higher32BitsOf(d3) ← r6
*/
vmov r5, r7, d4 /* r5 ← Lower32BitsOf(d4)
r7 ← Higher32BitsOf(d4)
*/Conversions
Sometimes we need to convert from an integer to a floating-point and the opposite. Note that some conversions may potentially lose precision, in particular when a floating point is converted to an integer. There is a single instruction vcvt with a suffix .T.S where T (target) and S (source) can be u32, s32, f32 and f64 (S must be different to T). Both registers must be floating point registers, so in order to convert integers to floating point or floating point to an integer value an extra vmov instruction will be required from or to an integer register before or after the conversion. Because of this, for a moment (between the two instructions) a floating point register will contain a value which is not a IEEE 754 value, bear this in mind.
vcvt.f64.f32 d0, s0 /* Converts s0 single-precision value
to a double-precision value and stores it in d0 */
vcvt.f32.f64 s0, d0 /* Converts d0 double-precision value
to a single-precision value and stores it in s0 */
vmov s0, r0 /* Bit copy from integer register r0 to s0 */
vcvt.f32.s32 s0, s0 /* Converts s0 signed integer value
to a single-precision value and stores it in s0 */
vmov s0, r0 /* Bit copy from integer register r0 to s0 */
vcvt.f32.u32 s0, s0 /* Converts s0 unsigned integer value
to a single-precision value and stores in s0 */
vmov s0, r0 /* Bit copy from integer register r0 to s0 */
vcvt.f64.s32 d0, s0 /* Converts r0 signed integer value
to a double-precision value and stores in d0 */
vmov s0, r0 /* Bit copy from integer register r0 to s0 */
vcvt.f64.u32 d0, s0 /* Converts s0 unsigned integer value
to a double-precision value and stores in d0 */Modifying fpscr
The special register fpscr, where len and stride are set, cannot be modified directly. Instead we have to load fpscr into a general purpose register using vmrs instruction. Then we operate on the register and move it back to the fpscr, using the vmsr instruction.
The value of len is stored in bits 16 to 18 of fpscr. The value of len is not directly stored directly in these bits. Instead, we have to subtract 1 before setting the bits. This is because len cannot be 0 (it does not make sense to operate 0 floating points). This way the value 000 in these bits means len = 1, 001 means len = 2, ..., 111 means len = 8. The following is a code that sets len to 8.
/* Set the len field of fpscr to be 8 (bits: 111) */
mov r5, #7 /* r5 ← 7. 7 is 111 in binary */
mov r5, r5, LSL #16 /* r5 ← r5 << 16 */
vmrs r4, fpscr /* r4 ← fpscr */
orr r4, r4, r5 /* r4 ← r4 | r5. Bitwise OR */
vmsr fpscr, r4 /* fpscr ← r4 */
stride is stored in bits 20 to 21 of fpscr. Similar to len, a value of 00 in these bits means stride = 1, 01 means stride = 2, 10 means stride = 3 and 11 means stride = 4.
Function call convention and floating-point registers
Since we have introduced new registers we should state how to use them when calling functions. The following rules apply for VFPv2 registers.
- Fields
lenandstrideoffpscrhave all their bits as zero at the entry of a function and those bits must be zero when leaving it. - We can pass floating point parameters using registers
s0-s15andd0-d7. Note that passing a double-precision after a single-precision may involve discarding an odd-numbered single-precision register (for instance we can uses0, andd1but note thats1will be unused). - All other floating point registers (
s16-s31andd8-d15) must have their values preserved upon leaving the function. Instructionsvpushandvpopcan be used for that. - If a function returns a floating-point value, the return register will be
s0ord0.
Finally a note about variadic functions like printf: you cannot pass a single-precision floating point to one of such functions. Only doubles can be passed. So you will need to convert the single-precision values into double-precision values. Note also that usual integer registers are used (r0-r3), so you will only be able to pass up to 2 double-precision values, the remaining must be passed on the stack. In particular for printf, since r0 contains the address of the string format, you will only be able to pass a double-precision in {r2,r3}.
Assembler
Make sure you pass the flag -mfpu=vfpv2 to as, otherwise it will not recognize the VFPv2 instructions.
Colophon
You may want to check this official quick reference card of VFP. Note that it includes also VFPv3 not available in the Raspberry Pi processor. Most of what is there has already been presented here although some minor details may have been omitted.
In the next chapter we will use these instructions in a full example.
That's all for today.