Exploring AArch64 assembler – Chapter 6
So far we know how to do some computations and access memory. Today we will learn how to alter the control flow of our program.
Implicit sequencing
Almost everyone would expect that a sequence of instructions, like the ones we've seen in previous chapters, would run one after the other. This is so fundamental that we can call it implicit sequencing: after one instruction has been executed, the next one does. This seems very obvious.
But what if we wanted to change this implicit sequencing with something else. What if we could, selectively, execute a subset of the instructions. Even better, what if we could run a subset of instructions depending on some condition?
Where the programs live
Programs live in memory. This seems so incredibly obvious. But in fact it is not. It is relatively simple to create specific digital circuits that perform very specific tasks. Their "program" does not live in memory, instead it is encoded directly in the circuit. But, while these circuits have a place, nowadays we can use CPUs that are very sophisticated circuits that can execute programs encoded as instructions.
If programs live in memory and are at their core a bunch of instructions, it means that the instructions will be addressable (each will have an address, once in memory). Given that, from a functional point of view, a CPU is at any given time executing only a single instruction, it may make sense to know which instruction is. The instruction itself, the particular binary code associated to it, is not very useful but its address is. So maybe we want to store the address of the current instruction somewhere in the CPU. And this is what it happens.
The program counter
The piece of memory that keeps track of the current instruction is called the program counter. In AArch64 the program counter is stored in a register called pc (for program counter). It is a 64-bit register with the address of the current instruction.
The pc tells the CPU which is the instruction that has to be executed. The CPU goes to memory, requests the 4 bytes at the address that the pc says. These 4 bytes are the instruction, recall that in AArch64 instructions are encoded in 32-bit. The instruction is then executed. When the execution of the instruction ends, the pc is incremented by 4 bytes. This is how implicit sequencing works. That's it.
But we may wonder, what if somehow rather than doing pc ← pc + 4 we could set the pc to something else when the instruction ends. Would the CPU execute some other instruction rather than the next one? The answer is yes. Except that in AArch64 we cannot write directly to the pc. But we can by doing branches.
Branches
Branches are instructions that are able to change the pc. By doing that they can alter the implicit sequencing of our program.
There are two kinds of branches: unconditional branches and conditional branches. Unconditional branches always set the pc to some value while conditional branches only do when some condition holds. When a branch sets the pc we say that the branch is taken. The address to where the pc is set is called the target of the branch. If a branch is not taken, then implicit sequencing applies.
Target of the branch
The target of the branch is an address. Addresses in assembler are most of the time represented using symbolic labels. So a branch will have at least one operand that is the target of the branch. Given that the address is encoded in the instruction there may be limitations of which labels we can use.
Unconditional branches
Unconditional branches are represented using the instruction b, for branch. The target of the branch is encoded as an offset of 27 bits, this is, an offset of ±128MiB. This offset, which is computed by the assembler tool, is added to the pc.
The following program will set the error condition to 3, even if there is an instruction that sets it to 4. The branch simply skips the execution of the second mov.
/* branch */
.text
.globl main
main:
mov w0, #3 // w0 ← 3
b jump // branch to label jump
mov w0, #4 // w0 ← 4
jump:
ret // end function
I will be writing labels in their own line (check main: and jump: above) which I think is a bit easier to read. I will also indent instruction after a label (check ret).
If we run this program effectively it sets the error code to 3.
$ ./branch ; echo $?
3Before you ask, yes, we can cause a program that never ends by jumping to ourselves. This will hang (use Ctrl-C to end it)
/* neverend.s */
.text
.globl main
main:
noprogress:
b noprogress // note: 'main' and 'noprogres'. are two different
// labels to the same address, doing 'b main' would hang
// as well
ret // it will never return!
At first it seems that unconditional branches are not very useful. They have their usefulness but we are still missing some details to be able to appreciate them. In a next chapter we will see another unconditional branch instruction called bl. That one is much more interesting, I promise.
Conditional branches
Conditional branches are a bit more interesting because the branch is taken only if some condition holds. Which kind of conditions?
AArch64 has a four flags. Each flag means some condition resulting from the execution of some instruction. Just a few instructions set these flags. For the current chapter we will consider only cmp. Also just a few instructions use these flags: among them conditional branch instructions.
Flags
As mentioned above there are 4 flags. They are N, Z, C, V. They are set as a result of executing one instruction that updates the flags. They have very specific meanings:
N(negative) is set if the result of the instruction yields a value that can be understood as a negative number. So positive and zero will have this flag unset.Z(zero) is set if the result of the instruction yields a value that is zero.C(carry) is set if the result of the instruction cannot be represented as an unsigned integer.V(overflow) is set if the result of the instruction cannot be represented as a signed integer.
The difference between flag C and V lies on the interpretation of the result. If we add two large positive integers and the result cannot be encoded as an unsigned integer, then C will be set. This happens, for instance, if we compute 231 + 231 and we want to keep the result in a 32-bit register: 232 cannot be represented with 32 bits. In this case C is set.
If we add two large positive integers or two large negative integers, it may happen that the result is too big (in absolute terms) to be encoded as a signed integer. For instance if we compute 230 + 230 the result is 231. If, again, we want to keep the result in a 32-bit register as a signed integer (i.e. two's complement) it simply cannot be encoded as such, so in this case V will be set but not C.
You may be wondering whether there is a case where C is set but not V. In fact there are many, when adding two signed integers, if one of them is negative and the other one is positive, C may be set but V will never be set (this operation cannot overflow in a signed integer interpretation). Consider for instance computing -1 + 2. The result is 1, so it fits in the range of signed integers, thus V is not enabled. But the encoding of the signed integer -1 interpreted as an unsigned integer is the value where all bits are 1. For a 32-bit operation this is 232-1. So, when we compute -1 + 2 we are actually doing 232-1 + 2, which would be 232+1. This number cannot be encoded in 32-bit as an unsigned integer, so the flag C would be enabled.
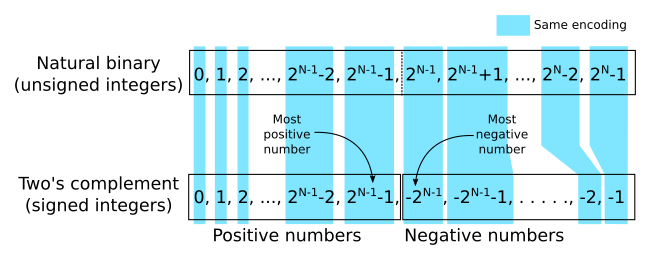 Unsigned and signed integers encoded in N-bits
Unsigned and signed integers encoded in N-bits
Utility of flags
Now that we see what the four flags mean, we can see some instructions that set them. Note that flags are set according to the result of some operation. Recall that for the purpose of the scope of this post we will consider only instruction cmp.
Instruction cmp does a comparison of the two operands. To do this it subtracts the second operand to the first operand (i.e. first - second) and updates the flags with the result of that subtraction. This subtraction is discarded, so the whole purpose of this operation is to update the flags.
Now consider several non obvious consequences of the comparison itself and how they are materialized in the flags. If we compare two registers that contain the same value, the subtraction will be zero, so the flag Z will be set. If the numbers are different, the result will be nonzero so Z will not be set. So the flag Z can be used to tell whether two values are the same or not.
If we are comparing integers we have to be more careful here. Let's start first with unsigned integers. In principle, subtracting one unsigned integer to another would only be well defined if the second is lower than the first. To avoid this problem, a two's complement subtraction is used instead. In two's complement a subtraction is just the usual addition where the second operand has been negated. If the first number is greater than the second, the result will be a positive number so the flag C will be set. If the first number is lower than the second, the addition will not overflow as it will stay as a negative number, so C will not be set.
If we are comparing two signed integers, the whole thing is a bit more complicated. If the first integer is larger than the second, a similar thing happens to unsigned integers, but now the result is interpreted as a signed number. This means that N should not be set in this case. And V should not be set either. But there are cases that the subtraction can cause a signed integer overflow: for instance if we subtract -1 to the largest positive representable integer. This is like adding 1 to that number. This causes an overflow and also the result happens to be interpreted as a negative, so N will be set. The reasoning here is that, if no overflow happens, the subtraction will look like a positive number. If overflow happens, the number must have become negative. So we can tell if the first number is larger than the second when N and V have the same value. Now consider the case where the first number is lower than the second, here the subtraction will always yield a negative number, except possibly when overflow happens. In this case the overflown number will be a positive one, consider for instance subtracting 1 to the smallest positive number, this is like adding -1. This will cause a signed integer overflow and the resulting number will be positive. So a way to tell whether a signed integer is lower than another one is that N and V have different values.
Condition codes
Now that we have some examples of the utility of the flags, we can talk about condition codes. A condition code is true when flags have some specific values. Condition codes are used by branching instructions, to determine if they are taken or not. Note that not all condition codes will be useful for a cmp operation (but they are for other instructions that set flags). I have marked in blue shade the most common condition codes.
| Name | Meaning | Condition flag |
|---|---|---|
| EQ | Values compare equal or the result of the operation is zero. | Z is set |
| NE | Values compare different or the result of the operation is non-zero. | Z is not set |
| GE | Greater or equal. Comparison of signed integers, the first operand is greater or equal than the second. | N and V are both set or both not set |
| GT | Greater. Comparison of signed integers, the first operand is greater than the second. | Z is not set. N and V are both set or both not set |
| LE | Lower or equal. Comparison of signed integers, the first operand is lower or equal than the second. | N is set and V is not set or the opposite |
| LT | Lower. Comparison of signed integers, the first operand is lower than the second. | Z is not set. N is set and V is not set or the opposite |
| CS | Carry set. For instance, an unsigned addition overflows. Not very useful with cmp |
C is set |
| CC | Carry clear. For instance, an unsigned addition does not overflow. Not very useful with cmp |
C is not set |
| MI | Minus. For instance, an addition or subtraction results a negative number. Not very useful with cmp |
N is set |
| PL | Positive or zero. For instance, an addition or subtraction results in a non negative number. Not very useful with cmp |
N is not set |
| VS | Overflow of signed integers. Not very useful with cmp |
V is set |
| VC | No overflow of signed integers. Not very useful with cmp |
V is not set |
| HI | Higher. Comparison of unsigned integers, the first operand is strictly greater than the second | C is set and Z is not set |
| HS | Higher or same. Comparison of unsigned integers, the first operand is greater or the same. Note that this is an alias of CS above. | C is set |
| LO | Lower. Comparison of unsigned integers, the first operand is strictly lower than the second. Note that this is an alias of CC above. | C is not set |
| LS | Lower or same. Comparison of unsigned integers, the first operand is lower or equal than the second. | Either C is not set or Z is set |
Conditional branch instruction
Ok, after all this prologue, we can now introduce the conditional branch instruction: b.cond
This instruction is a bit special in that one of its operands, the condition code, is represented in the name of the instruction. The cond part is the condition code and has to be one of the condition codes describe above.
Fortran arithmetic if
As an example of branches, let's see how we could implement a high-level programming language construct that alters the control flow of our program.
Fortran is a very old language invented in 1956. This means that has some odd constructions (in current practice, I guess at that moment they probably made sense). One of those constructions is the arithmetic if statement. The arithmetic if had this form
1
IF expression, label1, label2, label3
In Fortran the labels were represented with numbers from 0 to 99999 but we will use symbolic names instead. A Fortran program, when encounters an arithmetic if statement, evaluates the expression. The value of the expression is then compared to zero. If the expression is lower than zero, then the label1 is taken. If the expression evaluates to zero, the label2 is taken. Otherwise, if the expression evaluates to a value greater than zero the label3 is taken.
Let's assume, for simplicity, that the value of our expression is in w0. So the first thing we have to do is to compare it with zero.
1
2
3
arithmetic_if:
// code that evaluates the expression and sets its value in w0
cmp w0, #0 // compares w0 with 0 and updates the flags
Let's assume that w0 is a signed integer. The order of the comparisons is not important at first, so we can follow the description above.
4
5
6
7
8
9
10
11
12
13
14
15
16
17
b.lt label1 // if w0 < 0 then branch to label1
b.eq label2 // if w0 == 0 then branch to label2
b.gt label3 // if w0 > 1 then branch to label3
label1:
// code for label1
b end_of_arithmetic_if // branch to end_of_arithmetic_if
label2:
// code for label2
b end_of_arithmetic_if // branch to end_of_arithmetic_if
label3:
// code for label3
b end_of_arithmetic_if // branch to end_of_arithmetic_if
end_of_arithmetic_if:
// rest ouf our Fortran program :)
Of course we can save some branches if we make use of the layout of the instructions of our program.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
arithmetic_if:
// code that evaluates the expression and sets its value in w0
cmp w0, #0 // compares w0 with 0 and updates the flags
b.lt label1 // if w0 < 0 then branch to label1
b.eq label2 // if w0 == 0 then branch to label2
// code for label3
b end_of_arithmetic_if // branch to end_of_arithmetic_if
label1:
// code for label1
b end_of_arithmetic_if // branch to end_of_arithmetic_if
label2:
// code for label2
end_of_arithmetic_if:
// rest ouf our Fortran program :)
Ok, this post has been too long already. So let's stop here. In a next chapter we will put conditional branches at work by implementing a few common high level constructs.
That's all for today.