ARM assembler in Raspberry Pi – Chapter 14
In chapter 13 we saw the basic elements of VFPv2, the floating point subarchitecture of ARMv6. In this chapter we will implement a floating point matrix multiply using VFPv2.
Disclaimer: I advise you against using the code in this chapter in commercial-grade projects unless you fully review it for both correctness and precision.
Matrix multiply
Given two vectors v and w of rank r where v = <v0, v1, ... vr-1> and w = <w0, w1, ..., wr-1>, we define the dot product of v by w as the scalar v · w = v0×w0 + v1×w1 + ... + vr-1×wr-1.
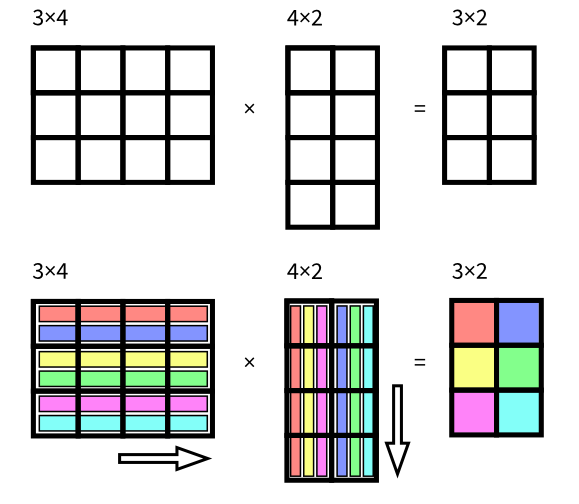
We can multiply a matrix A of n rows and m columns (n x m) by a matrix B of m rows and p columns (m x p). The result is a matrix of n rows and p columns. Matrix multiplication may seem complicated but actually it is not. Every element in the result matrix it is just the dot product (defined in the paragraph above) of the corresponding row of the matrix A by the corresponding column of the matrix B (this is why there must be as many columns in A as there are rows in B).
A straightforward implementation of the matrix multiplication in C is as follows.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
float A[N][M]; // N rows of M columns each row
float B[M][P]; // M rows of P columns each row
// Result
float C[N][P];
for (int i = 0; i < N; i++) // for each row of the result
{
for (int j = 0; j < P; j++) // and for each column
{
C[i][j] = 0; // Initialize to zero
// Now make the dot matrix of the row by the column
for (int k = 0; k < M; k++)
C[i][j] += A[i][k] * B[k][j];
}
}
In order to simplify the example, we will asume that both matrices A and B are square matrices of size n x n. This simplifies just a bit the algorithm.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
float A[N][N];
float B[N][N];
// Result
float C[N][N];
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
C[i][j] = 0;
for (int k = 0; k < N; k++)
C[i][j] += A[i][k] * B[k][j];
}
}
Matrix multiplication is an important operation used in many areas. For instance, in computer graphics is usually performed on 3x3 and 4x4 matrices representing 3D geometry. So we will try to make a reasonably fast version of it (we do not aim at making the best one, though).
A first improvement we want to do in this algorithm is making the loops perfectly nested. There are some technical reasons beyond the scope of this code for that. So we will get rid of the initialization of C[i][j] to 0, outside of the loop.
1
2
3
4
5
6
7
8
9
10
11
12
13
float A[N][N];
float B[M][N];
// Result
float C[N][N];
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
C[i][j] = 0;
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
for (int k = 0; k < N; k++)
C[i][j] += A[i][k] * B[k][j];
After this change, the interesting part of our algorithm, line 13, is inside a perfect nest of loops of depth 3.
Accessing a matrix
It is relatively straightforward to access an array of just one dimension, like in a[i]. Just get i, multiply it by the size in bytes of each element of the array and then add the address of a (the base address of the array). So, the address of a[i] is just a + ELEMENTSIZE*i.
Things get a bit more complicated when our array has more than one dimension, like a matrix or a cube. Given an access like a[i][j][k] we have to compute which element is denoted by [i][j][k]. This depends on whether the language is row-major order or column-major order. We assume row-major order here (like in C language). So [i][j][k] must denote k + j * NK + i * NK * NJ, where NK and NJ are the number of elements in every dimension. For instance, a three dimensional array of 3 x 4 x 5 elements, the element [1][2][3] is 3 + 2 * 5 + 1 * 5 * 4 = 23 (here NK = 5 and NJ = 4. Note that NI = 3 but we do not need it at all). We assume that our language indexes arrays starting from 0 (like C). If the language allows a lower bound other than 0, we first have to subtract the lower bound to get the position.
We can compute the position in a slightly better way if we reorder it. Instead of calculating k + j * NK + i * NK * NJ we will do k + NK * (j + NJ * i). This way all the calculus is just a repeated set of steps calculating x + Ni * y like in the example below.
/* Calculating the address of C[i][j][k] declared as int C[3][4][5] */
/* &C[i][j][k] is, thus, C + ELEMENTSIZE * ( k + NK * (j + NJ * i) ) */
// Assume i is in r4, j in r5 and k in r6 and the base address of C in r3 */
mov r8, #4 /* r8 ← NJ (Recall that NJ = 4) */
mul r7, r8, r4 /* r7 ← NJ * i */
add r7, r5, r7 /* r7 ← j + NJ * i */
mov r8, #5 /* r8 ← NK (Recall that NK = 5) */
mul r7, r8, r7 /* r7 ← NK * (j + NJ * i) */
add r7, r6, r7 /* r7 ← k + NK * (j + NJ + i) */
mov r8, #4 /* r8 ← ELEMENTSIZE (Recall that size of an int is 4 bytes) */
mul r7, r8, r7 /* r7 ← ELEMENTSIZE * ( k + NK * (j + NJ * i) ) */
add r7, r3, r7 /* r7 ← C + ELEMENTSIZE * ( k + NK * (j + NJ * i) ) */Naive matrix multiply of 4x4 single-precision
As a first step, let's implement a naive matrix multiply that follows the C algorithm above according to the letter.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
/* -- matmul.s */
.data
mat_A: .float 0.1, 0.2, 0.0, 0.1
.float 0.2, 0.1, 0.3, 0.0
.float 0.0, 0.3, 0.1, 0.5
.float 0.0, 0.6, 0.4, 0.1
mat_B: .float 4.92, 2.54, -0.63, -1.75
.float 3.02, -1.51, -0.87, 1.35
.float -4.29, 2.14, 0.71, 0.71
.float -0.95, 0.48, 2.38, -0.95
mat_C: .float 0.0, 0.0, 0.0, 0.0
.float 0.0, 0.0, 0.0, 0.0
.float 0.0, 0.0, 0.0, 0.0
.float 0.0, 0.0, 0.0, 0.0
.float 0.0, 0.0, 0.0, 0.0
format_result : .asciz "Matrix result is:\n%5.2f %5.2f %5.2f %5.2f\n%5.2f %5.2f %5.2f %5.2f\n%5.2f %5.2f %5.2f %5.2f\n%5.2f %5.2f %5.2f %5.2f\n"
.text
naive_matmul_4x4:
/* r0 address of A
r1 address of B
r2 address of C
*/
push {r4, r5, r6, r7, r8, lr} /* Keep integer registers */
/* First zero 16 single floating point */
/* In IEEE 754, all bits cleared means 0 */
mov r4, r2
mov r5, #16
mov r6, #0
b .Lloop_init_test
.Lloop_init :
str r6, [r4], +#4 /* *r4 ← r6 then r4 ← r4 + 4 */
.Lloop_init_test:
subs r5, r5, #1
bge .Lloop_init
/* We will use
r4 as i
r5 as j
r6 as k
*/
mov r4, #0 /* r4 ← 0 */
.Lloop_i: /* loop header of i */
cmp r4, #4 /* if r4 == 4 goto end of the loop i */
beq .Lend_loop_i
mov r5, #0 /* r5 ← 0 */
.Lloop_j: /* loop header of j */
cmp r5, #4 /* if r5 == 4 goto end of the loop j */
beq .Lend_loop_j
/* Compute the address of C[i][j] and load it into s0 */
/* Address of C[i][j] is C + 4*(4 * i + j) */
mov r7, r5 /* r7 ← r5. This is r7 ← j */
adds r7, r7, r4, LSL #2 /* r7 ← r7 + (r4 << 2).
This is r7 ← j + i * 4.
We multiply i by the row size (4 elements) */
adds r7, r2, r7, LSL #2 /* r7 ← r2 + (r7 << 2).
This is r7 ← C + 4*(j + i * 4)
We multiply (j + i * 4) by the size of the element.
A single-precision floating point takes 4 bytes.
*/
vldr s0, [r7] /* s0 ← *r7 */
mov r6, #0 /* r6 ← 0 */
.Lloop_k : /* loop header of k */
cmp r6, #4 /* if r6 == 4 goto end of the loop k */
beq .Lend_loop_k
/* Compute the address of a[i][k] and load it into s1 */
/* Address of a[i][k] is a + 4*(4 * i + k) */
mov r8, r6 /* r8 ← r6. This is r8 ← k */
adds r8, r8, r4, LSL #2 /* r8 ← r8 + (r4 << 2). This is r8 ← k + i * 4 */
adds r8, r0, r8, LSL #2 /* r8 ← r0 + (r8 << 2). This is r8 ← a + 4*(k + i * 4) */
vldr s1, [r8] /* s1 ← *r8 */
/* Compute the address of b[k][j] and load it into s2 */
/* Address of b[k][j] is b + 4*(4 * k + j) */
mov r8, r5 /* r8 ← r5. This is r8 ← j */
adds r8, r8, r6, LSL #2 /* r8 ← r8 + (r6 << 2). This is r8 ← j + k * 4 */
adds r8, r1, r8, LSL #2 /* r8 ← r1 + (r8 << 2). This is r8 ← b + 4*(j + k * 4) */
vldr s2, [r8] /* s1 ← *r8 */
vmul.f32 s3, s1, s2 /* s3 ← s1 * s2 */
vadd.f32 s0, s0, s3 /* s0 ← s0 + s3 */
add r6, r6, #1 /* r6 ← r6 + 1 */
b .Lloop_k /* next iteration of loop k */
.Lend_loop_k: /* Here ends loop k */
vstr s0, [r7] /* Store s0 back to C[i][j] */
add r5, r5, #1 /* r5 ← r5 + 1 */
b .Lloop_j /* next iteration of loop j */
.Lend_loop_j: /* Here ends loop j */
add r4, r4, #1 /* r4 ← r4 + 1 */
b .Lloop_i /* next iteration of loop i */
.Lend_loop_i: /* Here ends loop i */
pop {r4, r5, r6, r7, r8, lr} /* Restore integer registers */
bx lr /* Leave function */
.globl main
main:
push {r4, r5, r6, lr} /* Keep integer registers */
vpush {d0-d1} /* Keep floating point registers */
/* Prepare call to naive_matmul_4x4 */
ldr r0, addr_mat_A /* r0 ← a */
ldr r1, addr_mat_B /* r1 ← b */
ldr r2, addr_mat_C /* r2 ← c */
bl naive_matmul_4x4
/* Now print the result matrix */
ldr r4, addr_mat_C /* r4 ← c */
vldr s0, [r4] /* s0 ← *r4. This is s0 ← c[0][0] */
vcvt.f64.f32 d1, s0 /* Convert it into a double-precision
d1 ← s0
*/
vmov r2, r3, d1 /* {r2,r3} ← d1 */
mov r6, sp /* Remember the stack pointer, we need it to restore it back later */
/* r6 ← sp */
mov r5, #1 /* We will iterate from 1 to 15 (because the 0th item has already been handled */
add r4, r4, #60 /* Go to the last item of the matrix c, this is c[3][3] */
.Lloop:
vldr s0, [r4] /* s0 ← *r4. Load the current item */
vcvt.f64.f32 d1, s0 /* Convert it into a double-precision
d1 ← s0
*/
sub sp, sp, #8 /* Make room in the stack for the double-precision */
vstr d1, [sp] /* Store the double precision in the top of the stack */
sub r4, r4, #4 /* Move to the previous element in the matrix */
add r5, r5, #1 /* One more item has been handled */
cmp r5, #16 /* if r5 != 16 go to next iteration of the loop */
bne .Lloop
ldr r0, addr_format_result /* r0 ← &format_result */
bl printf /* call printf */
mov sp, r6 /* Restore the stack after the call */
mov r0, #0
vpop {d0-d1}
pop {r4, r5, r6, lr}
bx lr
addr_mat_A : .word mat_A
addr_mat_B : .word mat_B
addr_mat_C : .word mat_C
addr_format_result : .word format_result
That's a lot of code but it is not complicated. Unfortunately computing the address of the array takes an important number of instructions. In our naive_matmul_4x4 we have the three loops i, j and k of the C algorithm. We compute the address of C[i][j] in the loop j (there is no need to compute it every time in the loop k) in lines 52 to 63. The value contained in C[i][j] is then loaded into s0. In each iteration of loop k we load A[i][k] and B[k][j] in s1 and s2 respectively (lines 70 to 82). After the loop k ends, we can store s0 back to the array position (kept in r7, line 90)
In order to print the result matrix we have to pass 16 floating points to printf. Unfortunately, as stated in chapter 13, we have to first convert them into double-precision before passing them. Note also that the first single-precision can be passed using registers r2 and r3. All the remaining must be passed on the stack and do not forget that the stack parameters must be passed in opposite order. This is why once the first element of the C matrix has been loaded in {r2,r3} (lines 117 to 120) we advance 60 bytes r4. This is C[3][3], the last element of the matrix C. We load the single-precision, convert it into double-precision, push it in the stack and then move backwards register r4, to the previous element in the matrix (lines 128 to 137). Observe that we use r6 as a marker of the stack, since we need to restore the stack once printf returns (line 122 and line 141). Of course we could avoid using r6 and instead do add sp, sp, #120 since this is exactly the amount of bytes we push to the stack (15 values of double-precision, each taking 8 bytes).
I have not chosen the values of the two matrices randomly. The second one is (approximately) the inverse of the first. This way we will get the identity matrix (a matrix with all zeros but a diagonal of ones). Due to rounding issues the result matrix will not be the identity, but it will be pretty close. Let's run the program.
$ ./matmul
Matrix result is:
1.00 -0.00 0.00 0.00
-0.00 1.00 0.00 -0.00
0.00 0.00 1.00 0.00
0.00 -0.00 0.00 1.00Vectorial approach
The algorithm we are trying to implement is fine but it is not the most optimizable. The problem lies in the way the loop k accesses the elements. Access A[i][k] is eligible for a multiple load as A[i][k] and A[i][k+1] are contiguous elements in memory. This way we could entirely avoid all the loop k and perform a 4 element load from A[i][0] to A[i][3]. The access B[k][j] does not allow that since elements B[k][j] and B[k+1][j] have a full row inbetween. This is a strided access (the stride here is a full row of 4 elements, this is 16 bytes), VFPv2 does not allow a strided multiple load, so we will have to load one by one.. Once we have all the elements of the loop k loaded, we can do a vector multiplication and a sum.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
naive_vectorial_matmul_4x4:
/* r0 address of A
r1 address of B
r2 address of C
*/
push {r4, r5, r6, r7, r8, lr} /* Keep integer registers */
vpush {s16-s19} /* Floating point registers starting from s16 must be preserved */
vpush {s24-s27}
/* First zero 16 single floating point */
/* In IEEE 754, all bits cleared means 0 */
mov r4, r2
mov r5, #16
mov r6, #0
b .L1_loop_init_test
.L1_loop_init :
str r6, [r4], +#4 /* *r4 ← r6 then r4 ← r4 + 4 */
.L1_loop_init_test:
subs r5, r5, #1
bge .L1_loop_init
/* Set the LEN field of FPSCR to be 4 (value 3) */
mov r5, #0b011 /* r5 ← 3 */
mov r5, r5, LSL #16 /* r5 ← r5 << 16 */
fmrx r4, fpscr /* r4 ← fpscr */
orr r4, r4, r5 /* r4 ← r4 | r5 */
fmxr fpscr, r4 /* fpscr ← r4 */
/* We will use
r4 as i
r5 as j
r6 as k
*/
mov r4, #0 /* r4 ← 0 */
.L1_loop_i: /* loop header of i */
cmp r4, #4 /* if r4 == 4 goto end of the loop i */
beq .L1_end_loop_i
mov r5, #0 /* r5 ← 0 */
.L1_loop_j: /* loop header of j */
cmp r5, #4 /* if r5 == 4 goto end of the loop j */
beq .L1_end_loop_j
/* Compute the address of C[i][j] and load it into s0 */
/* Address of C[i][j] is C + 4*(4 * i + j) */
mov r7, r5 /* r7 ← r5. This is r7 ← j */
adds r7, r7, r4, LSL #2 /* r7 ← r7 + (r4 << 2).
This is r7 ← j + i * 4.
We multiply i by the row size (4 elements) */
adds r7, r2, r7, LSL #2 /* r7 ← r2 + (r7 << 2).
This is r7 ← C + 4*(j + i * 4)
We multiply (j + i * 4) by the size of the element.
A single-precision floating point takes 4 bytes.
*/
/* Compute the address of a[i][0] */
mov r8, r4, LSL #2
adds r8, r0, r8, LSL #2
vldmia r8, {s8-s11} /* Load {s8,s9,s10,s11} ← {a[i][0], a[i][1], a[i][2], a[i][3]} */
/* Compute the address of b[0][j] */
mov r8, r5 /* r8 ← r5. This is r8 ← j */
adds r8, r1, r8, LSL #2 /* r8 ← r1 + (r8 << 2). This is r8 ← b + 4*(j) */
vldr s16, [r8] /* s16 ← *r8. This is s16 ← b[0][j] */
vldr s17, [r8, #16] /* s17 ← *(r8 + 16). This is s17 ← b[1][j] */
vldr s18, [r8, #32] /* s18 ← *(r8 + 32). This is s17 ← b[2][j] */
vldr s19, [r8, #48] /* s19 ← *(r8 + 48). This is s17 ← b[3][j] */
vmul.f32 s24, s8, s16 /* {s24,s25,s26,s27} ← {s8,s9,s10,s11} * {s16,s17,s18,s19} */
vmov.f32 s0, s24 /* s0 ← s24 */
vadd.f32 s0, s0, s25 /* s0 ← s0 + s25 */
vadd.f32 s0, s0, s26 /* s0 ← s0 + s26 */
vadd.f32 s0, s0, s27 /* s0 ← s0 + s27 */
vstr s0, [r7] /* Store s0 back to C[i][j] */
add r5, r5, #1 /* r5 ← r5 + 1 */
b .L1_loop_j /* next iteration of loop j */
.L1_end_loop_j: /* Here ends loop j */
add r4, r4, #1 /* r4 ← r4 + 1 */
b .L1_loop_i /* next iteration of loop i */
.L1_end_loop_i: /* Here ends loop i */
/* Set the LEN field of FPSCR back to 1 (value 0) */
mov r5, #0b011 /* r5 ← 3 */
mvn r5, r5, LSL #16 /* r5 ← ~(r5 << 16) */
fmrx r4, fpscr /* r4 ← fpscr */
and r4, r4, r5 /* r4 ← r4 & r5 */
fmxr fpscr, r4 /* fpscr ← r4 */
vpop {s24-s27} /* Restore preserved floating registers */
vpop {s16-s19}
pop {r4, r5, r6, r7, r8, lr} /* Restore integer registers */
bx lr /* Leave function */
With this approach we can entirely remove the loop k, as we do 4 operations at once. Note that we have to modify fpscr so the field len is set to 4 (and restore it back to 1 when leaving the function).
Fill the registers
In the previous version we are not exploiting all the registers of VFPv2. Each rows takes 4 registers and so does each column, so we end using only 8 registers plus 4 for the result and one in the bank 0 for the summation. We got rid the loop k to process C[i][j] at once. What if we processed C[i][j] and C[i][j+1] at the same time? This way we can fill all the 8 registers in each bank.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
naive_vectorial_matmul_2_4x4:
/* r0 address of A
r1 address of B
r2 address of C
*/
push {r4, r5, r6, r7, r8, lr} /* Keep integer registers */
vpush {s16-s31} /* Floating point registers starting from s16 must be preserved */
/* First zero 16 single floating point */
/* In IEEE 754, all bits cleared means 0 */
mov r4, r2
mov r5, #16
mov r6, #0
b .L2_loop_init_test
.L2_loop_init :
str r6, [r4], +#4 /* *r4 ← r6 then r4 ← r4 + 4 */
.L2_loop_init_test:
subs r5, r5, #1
bge .L2_loop_init
/* Set the LEN field of FPSCR to be 4 (value 3) */
mov r5, #0b011 /* r5 ← 3 */
mov r5, r5, LSL #16 /* r5 ← r5 << 16 */
fmrx r4, fpscr /* r4 ← fpscr */
orr r4, r4, r5 /* r4 ← r4 | r5 */
fmxr fpscr, r4 /* fpscr ← r4 */
/* We will use
r4 as i
r5 as j
*/
mov r4, #0 /* r4 ← 0 */
.L2_loop_i: /* loop header of i */
cmp r4, #4 /* if r4 == 4 goto end of the loop i */
beq .L2_end_loop_i
mov r5, #0 /* r5 ← 0 */
.L2_loop_j: /* loop header of j */
cmp r5, #4 /* if r5 == 4 goto end of the loop j */
beq .L2_end_loop_j
/* Compute the address of C[i][j] and load it into s0 */
/* Address of C[i][j] is C + 4*(4 * i + j) */
mov r7, r5 /* r7 ← r5. This is r7 ← j */
adds r7, r7, r4, LSL #2 /* r7 ← r7 + (r4 << 2).
This is r7 ← j + i * 4.
We multiply i by the row size (4 elements) */
adds r7, r2, r7, LSL #2 /* r7 ← r2 + (r7 << 2).
This is r7 ← C + 4*(j + i * 4)
We multiply (j + i * 4) by the size of the element.
A single-precision floating point takes 4 bytes.
*/
/* Compute the address of a[i][0] */
mov r8, r4, LSL #2
adds r8, r0, r8, LSL #2
vldmia r8, {s8-s11} /* Load {s8,s9,s10,s11} ← {a[i][0], a[i][1], a[i][2], a[i][3]} */
/* Compute the address of b[0][j] */
mov r8, r5 /* r8 ← r5. This is r8 ← j */
adds r8, r1, r8, LSL #2 /* r8 ← r1 + (r8 << 2). This is r8 ← b + 4*(j) */
vldr s16, [r8] /* s16 ← *r8. This is s16 ← b[0][j] */
vldr s17, [r8, #16] /* s17 ← *(r8 + 16). This is s17 ← b[1][j] */
vldr s18, [r8, #32] /* s18 ← *(r8 + 32). This is s17 ← b[2][j] */
vldr s19, [r8, #48] /* s19 ← *(r8 + 48). This is s17 ← b[3][j] */
/* Compute the address of b[0][j+1] */
add r8, r5, #1 /* r8 ← r5 + 1. This is r8 ← j + 1*/
adds r8, r1, r8, LSL #2 /* r8 ← r1 + (r8 << 2). This is r8 ← b + 4*(j + 1) */
vldr s20, [r8] /* s20 ← *r8. This is s20 ← b[0][j + 1] */
vldr s21, [r8, #16] /* s21 ← *(r8 + 16). This is s21 ← b[1][j + 1] */
vldr s22, [r8, #32] /* s22 ← *(r8 + 32). This is s22 ← b[2][j + 1] */
vldr s23, [r8, #48] /* s23 ← *(r8 + 48). This is s23 ← b[3][j + 1] */
vmul.f32 s24, s8, s16 /* {s24,s25,s26,s27} ← {s8,s9,s10,s11} * {s16,s17,s18,s19} */
vmov.f32 s0, s24 /* s0 ← s24 */
vadd.f32 s0, s0, s25 /* s0 ← s0 + s25 */
vadd.f32 s0, s0, s26 /* s0 ← s0 + s26 */
vadd.f32 s0, s0, s27 /* s0 ← s0 + s27 */
vmul.f32 s28, s8, s20 /* {s28,s29,s30,s31} ← {s8,s9,s10,s11} * {s20,s21,s22,s23} */
vmov.f32 s1, s28 /* s1 ← s28 */
vadd.f32 s1, s1, s29 /* s1 ← s1 + s29 */
vadd.f32 s1, s1, s30 /* s1 ← s1 + s30 */
vadd.f32 s1, s1, s31 /* s1 ← s1 + s31 */
vstmia r7, {s0-s1} /* {C[i][j], C[i][j+1]} ← {s0, s1} */
add r5, r5, #2 /* r5 ← r5 + 2 */
b .L2_loop_j /* next iteration of loop j */
.L2_end_loop_j: /* Here ends loop j */
add r4, r4, #1 /* r4 ← r4 + 1 */
b .L2_loop_i /* next iteration of loop i */
.L2_end_loop_i: /* Here ends loop i */
/* Set the LEN field of FPSCR back to 1 (value 0) */
mov r5, #0b011 /* r5 ← 3 */
mvn r5, r5, LSL #16 /* r5 ← ~(r5 << 16) */
fmrx r4, fpscr /* r4 ← fpscr */
and r4, r4, r5 /* r4 ← r4 & r5 */
fmxr fpscr, r4 /* fpscr ← r4 */
vpop {s16-s31} /* Restore preserved floating registers */
pop {r4, r5, r6, r7, r8, lr} /* Restore integer registers */
bx lr /* Leave function */
Note that because we now process j and j + 1, r5 (j) is now increased by 2 at the end of the loop. This is usually known as loop unrolling and it is always legal to do. We do more than one iteration of the original loop in the unrolled loop. The amount of iterations of the original loop we do in the unrolled loop is the unroll factor. In this case since the number of iterations (4) perfectly divides the unrolling factor (2) we do not need an extra loop for the remainder iterations (the remainder loop has one less iteration than the value of the unrolling factor).
As you can see, the accesses to b[k][j] and b[k][j+1] are starting to become tedious. Maybe we should change a bit more the matrix multiply algorithm.
Reorder the accesses
Is there a way we can mitigate the strided accesses to the matrix B? Yes, there is one, we only have to permute the loop nest i, j, k into the loop nest k, i, j. Now you may be wondering if this is legal. Well, checking for the legality of these things is beyond the scope of this post so you will have to trust me here. Such permutation is fine. What does this mean? Well, it means that our algorithm will now look like this.
1
2
3
4
5
6
7
8
9
10
11
12
13
float A[N][N];
float B[M][N];
// Result
float C[N][N];
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
C[i][j] = 0;
for (int k = 0; k < N; k++)
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
C[i][j] += A[i][k] * B[k][j];
This may seem not very useful, but note that, since now k is in the outermost loop, now it is easier to use vectorial instructions.
for (int k = 0; k < N; k++)
for (int i = 0; i < N; i++)
{
C[i][0] += A[i][k] * B[k][0];
C[i][1] += A[i][k] * B[k][1];
C[i][2] += A[i][k] * B[k][2];
C[i][3] += A[i][k] * B[k][3];
}
If you remember the chapter 13, VFPv2 instructions have a mixed mode when the Rsource2 register is in bank 0. This case makes a perfect match: we can load C[i][0..3] and B[k][0..3] with a load multiple and then load A[i][k] in a register of the bank 0. Then we can make multiply A[i][k]*B[k][0..3] and add the result to C[i][0..3]. As a bonus, the number of instructions is much lower.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
better_vectorial_matmul_4x4:
/* r0 address of A
r1 address of B
r2 address of C
*/
push {r4, r5, r6, r7, r8, lr} /* Keep integer registers */
vpush {s16-s19} /* Floating point registers starting from s16 must be preserved */
vpush {s24-s27}
/* First zero 16 single floating point */
/* In IEEE 754, all bits cleared means 0 */
mov r4, r2
mov r5, #16
mov r6, #0
b .L3_loop_init_test
.L3_loop_init :
str r6, [r4], +#4 /* *r4 ← r6 then r4 ← r4 + 4 */
.L3_loop_init_test:
subs r5, r5, #1
bge .L3_loop_init
/* Set the LEN field of FPSCR to be 4 (value 3) */
mov r5, #0b011 /* r5 ← 3 */
mov r5, r5, LSL #16 /* r5 ← r5 << 16 */
fmrx r4, fpscr /* r4 ← fpscr */
orr r4, r4, r5 /* r4 ← r4 | r5 */
fmxr fpscr, r4 /* fpscr ← r4 */
/* We will use
r4 as k
r5 as i
*/
mov r4, #0 /* r4 ← 0 */
.L3_loop_k: /* loop header of k */
cmp r4, #4 /* if r4 == 4 goto end of the loop k */
beq .L3_end_loop_k
mov r5, #0 /* r5 ← 0 */
.L3_loop_i: /* loop header of i */
cmp r5, #4 /* if r5 == 4 goto end of the loop i */
beq .L3_end_loop_i
/* Compute the address of C[i][0] */
/* Address of C[i][0] is C + 4*(4 * i) */
add r7, r2, r5, LSL #4 /* r7 ← r2 + (r5 << 4). This is r7 ← c + 4*4*i */
vldmia r7, {s8-s11} /* Load {s8,s9,s10,s11} ← {c[i][0], c[i][1], c[i][2], c[i][3]} */
/* Compute the address of A[i][k] */
/* Address of A[i][k] is A + 4*(4*i + k) */
add r8, r4, r5, LSL #2 /* r8 ← r4 + r5 << 2. This is r8 ← k + 4*i */
add r8, r0, r8, LSL #2 /* r8 ← r0 + r8 << 2. This is r8 ← a + 4*(k + 4*i) */
vldr s0, [r8] /* Load s0 ← a[i][k] */
/* Compute the address of B[k][0] */
/* Address of B[k][0] is B + 4*(4*k) */
add r8, r1, r4, LSL #4 /* r8 ← r1 + r4 << 4. This is r8 ← b + 4*(4*k) */
vldmia r8, {s16-s19} /* Load {s16,s17,s18,s19} ← {b[k][0], b[k][1], b[k][2], b[k][3]} */
vmul.f32 s24, s16, s0 /* {s24,s25,s26,s27} ← {s16,s17,s18,s19} * {s0,s0,s0,s0} */
vadd.f32 s8, s8, s24 /* {s8,s9,s10,s11} ← {s8,s9,s10,s11} + {s24,s25,s26,s7} */
vstmia r7, {s8-s11} /* Store {c[i][0], c[i][1], c[i][2], c[i][3]} ← {s8,s9,s10,s11} */
add r5, r5, #1 /* r5 ← r5 + 1. This is i = i + 1 */
b .L3_loop_i /* next iteration of loop i */
.L3_end_loop_i: /* Here ends loop i */
add r4, r4, #1 /* r4 ← r4 + 1. This is k = k + 1 */
b .L3_loop_k /* next iteration of loop k */
.L3_end_loop_k: /* Here ends loop k */
/* Set the LEN field of FPSCR back to 1 (value 0) */
mov r5, #0b011 /* r5 ← 3 */
mvn r5, r5, LSL #16 /* r5 ← ~(r5 << 16) */
fmrx r4, fpscr /* r4 ← fpscr */
and r4, r4, r5 /* r4 ← r4 & r5 */
fmxr fpscr, r4 /* fpscr ← r4 */
vpop {s24-s27} /* Restore preserved floating registers */
vpop {s16-s19}
pop {r4, r5, r6, r7, r8, lr} /* Restore integer registers */
bx lr /* Leave function */
As adding after a multiplication is a relatively usual sequence, we can replace the sequence
55
56
vmul.f32 s24, s16, s0 /* {s24,s25,s26,s27} ← {s16,s17,s18,s19} * {s0,s0,s0,s0} */
vadd.f32 s8, s8, s24 /* {s8,s9,s10,s11} ← {s8,s9,s10,s11} + {s24,s25,s26,s7} */
with a single instruction vmla (multiply and add).
55
vmla.f32 s8, s16, s0 /* {s8,s9,s10,s11} ← {s8,s9,s10,s11} + ({s16,s17,s18,s19} * {s0,s0,s0,s0}) */
Now we can also unroll the loop i, again with an unrolling factor of 2. This would give us the best version.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
best_vectorial_matmul_4x4:
/* r0 address of A
r1 address of B
r2 address of C
*/
push {r4, r5, r6, r7, r8, lr} /* Keep integer registers */
vpush {s16-s19} /* Floating point registers starting from s16 must be preserved */
/* First zero 16 single floating point */
/* In IEEE 754, all bits cleared means 0 */
mov r4, r2
mov r5, #16
mov r6, #0
b .L4_loop_init_test
.L4_loop_init :
str r6, [r4], +#4 /* *r4 ← r6 then r4 ← r4 + 4 */
.L4_loop_init_test:
subs r5, r5, #1
bge .L4_loop_init
/* Set the LEN field of FPSCR to be 4 (value 3) */
mov r5, #0b011 /* r5 ← 3 */
mov r5, r5, LSL #16 /* r5 ← r5 << 16 */
fmrx r4, fpscr /* r4 ← fpscr */
orr r4, r4, r5 /* r4 ← r4 | r5 */
fmxr fpscr, r4 /* fpscr ← r4 */
/* We will use
r4 as k
r5 as i
*/
mov r4, #0 /* r4 ← 0 */
.L4_loop_k: /* loop header of k */
cmp r4, #4 /* if r4 == 4 goto end of the loop k */
beq .L4_end_loop_k
mov r5, #0 /* r5 ← 0 */
.L4_loop_i: /* loop header of i */
cmp r5, #4 /* if r5 == 4 goto end of the loop i */
beq .L4_end_loop_i
/* Compute the address of C[i][0] */
/* Address of C[i][0] is C + 4*(4 * i) */
add r7, r2, r5, LSL #4 /* r7 ← r2 + (r5 << 4). This is r7 ← c + 4*4*i */
vldmia r7, {s8-s15} /* Load {s8,s9,s10,s11,s12,s13,s14,s15}
← {c[i][0], c[i][1], c[i][2], c[i][3]
c[i+1][0], c[i+1][1], c[i+1][2], c[i+1][3]} */
/* Compute the address of A[i][k] */
/* Address of A[i][k] is A + 4*(4*i + k) */
add r8, r4, r5, LSL #2 /* r8 ← r4 + r5 << 2. This is r8 ← k + 4*i */
add r8, r0, r8, LSL #2 /* r8 ← r0 + r8 << 2. This is r8 ← a + 4*(k + 4*i) */
vldr s0, [r8] /* Load s0 ← a[i][k] */
vldr s1, [r8, #16] /* Load s1 ← a[i+1][k] */
/* Compute the address of B[k][0] */
/* Address of B[k][0] is B + 4*(4*k) */
add r8, r1, r4, LSL #4 /* r8 ← r1 + r4 << 4. This is r8 ← b + 4*(4*k) */
vldmia r8, {s16-s19} /* Load {s16,s17,s18,s19} ← {b[k][0], b[k][1], b[k][2], b[k][3]} */
vmla.f32 s8, s16, s0 /* {s8,s9,s10,s11} ← {s8,s9,s10,s11} + ({s16,s17,s18,s19} * {s0,s0,s0,s0}) */
vmla.f32 s12, s16, s1 /* {s12,s13,s14,s15} ← {s12,s13,s14,s15} + ({s16,s17,s18,s19} * {s1,s1,s1,s1}) */
vstmia r7, {s8-s15} /* Store {c[i][0], c[i][1], c[i][2], c[i][3],
c[i+1][0], c[i+1][1], c[i+1][2]}, c[i+1][3] }
← {s8,s9,s10,s11,s12,s13,s14,s15} */
add r5, r5, #2 /* r5 ← r5 + 2. This is i = i + 2 */
b .L4_loop_i /* next iteration of loop i */
.L4_end_loop_i: /* Here ends loop i */
add r4, r4, #1 /* r4 ← r4 + 1. This is k = k + 1 */
b .L4_loop_k /* next iteration of loop k */
.L4_end_loop_k: /* Here ends loop k */
/* Set the LEN field of FPSCR back to 1 (value 0) */
mov r5, #0b011 /* r5 ← 3 */
mvn r5, r5, LSL #16 /* r5 ← ~(r5 << 16) */
fmrx r4, fpscr /* r4 ← fpscr */
and r4, r4, r5 /* r4 ← r4 & r5 */
fmxr fpscr, r4 /* fpscr ← r4 */
vpop {s16-s19} /* Restore preserved floating registers */
pop {r4, r5, r6, r7, r8, lr} /* Restore integer registers */
bx lr /* Leave function */
Comparing versions
Out of curiosity I tested the versions, to see which one was faster.
The benchmark consists on repeatedly calling the multiplication matrix function 221 times (actually 221-1 because of a typo, see the code) in order to magnify differences. While the input should be randomized as well for a better benchmark, the benchmark more or less models contexts where a matrix multiplication is performed many times (for instance in graphics).
This is the skeleton of the benchmark.
main:
push {r4, lr}
ldr r0, addr_mat_A /* r0 ← a */
ldr r1, addr_mat_B /* r1 ← b */
ldr r2, addr_mat_C /* r2 ← c */
mov r4, #1
mov r4, r4, LSL #21
.Lmain_loop_test:
bl <<tested-matmul-routine>> /* Change here with the matmul you want to test */
subs r4, r4, #1
bne .Lmain_loop_test /* I should have written 'bge' here,
but I cannot change it without
having to run the benchmarks again :) */
mov r0, #0
pop {r4, lr}
bx lr
Here are the results. The one we named the best turned to actually deserve that name.
| Version | Time (seconds) |
|---|---|
| naive_matmul_4x4 | 6.41 |
| naive_vectorial_matmul_4x4 | 3.51 |
| naive_vectorial_matmul_2_4x4 | 2.87 |
| better_vectorial_matmul_4x4 | 2.59 |
| best_vectorial_matmul_4x4 | 1.51 |
That's all for today.